1.1 수학과 파이썬 복습
1.1.1 벡터와 행렬

벡터 - 크기와 방향을 가진 양, 1차원 배열
행렬 - 2차원 형태로 늘어선 것, 2차원 배열, 가로줄 행row, 열column

열벡터 - 숫자를 세로로 나열
행벡터 - 숫자를 가로로 나열
>>>import numpy as np
>>>x = np.array([1, 2, 3])
>>>x.__class__ # 클래스 이름 표시
<class 'numpy.ndarray'>
>>>x.shape
(3,)
>>>x.ndim
1
>>>W = np.array([[1,2,3],[4,5,6]])
>>>W.shape
(2,3)
>>>W.dim
21.1.2 행렬의 원소별 연산
>>>W = np.array([[1,2,3],[4,5,6]])
>>>X = np.array([[0,1,2],[3,4,5]])
>>>W + X
array([[1,3,5],
[7,9,11]])
>>>W * X
array([[0,2,6],
[12,20,30]])1.1.3 브로드캐스트
>>>A = np.array([[1,2],[3,4])
>>>A * 10
array([[1,3,5],
[7,9,11]])
>>>A = np.array([[1,2],[3,4])
>>>B = np.array([10,20])
>>>A * B
array([[10,40],
[30,80]])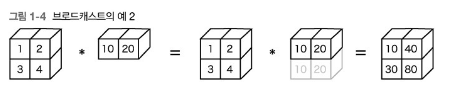
1.1.4 벡터의 내적과 행렬의 곱

벡터의 내적은 두 벡터에서 대응하는 원소들의 곱을 모두 더한 것

>>>a = np.array([[1,2,3])
>>>b = np.array([[4,5,6])
>>>np.dot(a,b)
32
>>>A = np.array([[1,2],[3,4])
>>>B = np.array([[5,6],[7,8])
>>>np.matnul(A,B)
array([[19,22],
[43,50]])✏️ np.dot과 np.matnul의 차이
2차원 행렬곱의 경우 결과가 동일하나 3차원 이상의 행렬끼리 곱할 때 다른 결과를 보여줌>> import numpy as np >> A = np.arange(2*3*4).reshape((2,3,4)) >> B = np.arange(2*3*4).reshape((2,4,3)) >> np.dot(A,B).shape (2, 3, 2, 3) >> np.matmul(A,B).shape (2, 3, 3)
- np.dot(A,B)의 경우 A의 마지막 축과 B의 뒤에서 두번째 축과의 내적으로 계산_dot product
- (2,3,4) (2,4,3)
- np.matmul(A,B)의 경우 2차원 이상일 시 마지막 2개의 축으로 이루어진 행렬을 나머지 축에 따라 쌓음_matrix product
- (2,3,4) 인 경우 A를 (3*4)핼렬을 2개 가지고 있음
내용 참고 및 출처: numpy에서 dot과 matmul의 차이
1.1.5 행렬 형상 확인

행렬과 벡터를 사용해 계산할 때는 '형상확인'을 진행해야함
1.2 신경망의 추론
1.2.1 신경망 추론 전체 그림
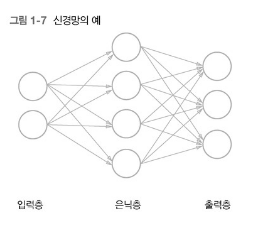
ㅇ은 뉴런이고 화살표에 가중치가 각 뉴런의 값을 곱하여 다음 뉴런의 입력됨
각 층에 이전 뉴런 값에 영향받지 않는 편향이 있고,
그림의 신경망은 인전하는 층의 모든 뉴런과 연결되어 있는 완전연결계층

뉴런 h 입력층 데이터 x 가중치 w 편향 b

완전연결계층이 수행하는 변환

간소화
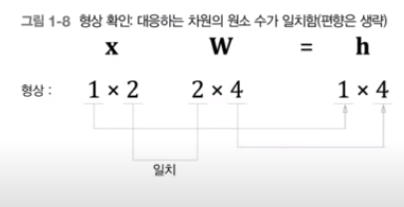
행렬 곱에서는 차원 원소수가 일치해야함
형상을 보면 올바른 변환인지 확인할 수 있음
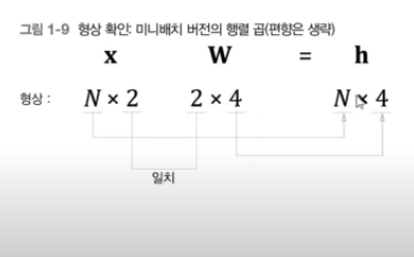
그림과 같이 미니배치가 올바르게 변환 되었는지 알수 있음
>>> improt numpy as np
>>>W1 = np.random.randn(2,4) # 가중치
>>>b1 = np.random.randn(4) # 편향
>>>x = np.random.randn(10,2) # 입력
>>>h = np.mutmul(x,W1) + b1randn(a,b) 평균0, 표준편차1의 가우시안 표준정규분포 난수로 matrix array(a,b)생성
-> array([0.12353587, 0.24684352, -0.02461143, -1.53057335])
여기서 완전연결계층에 의한 변환은 '선형' 변환으로 '비선형' 성을 부여하기 위해 활성화 함수 이용
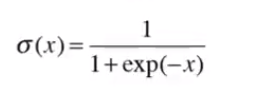
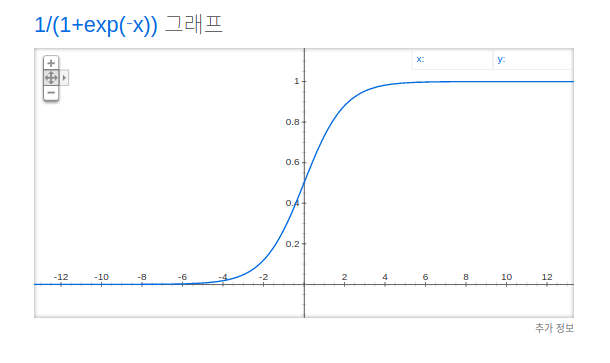
def sigmoid(x):
return 1 / (1 + np.exp(-x)) # exp() 지수함수 연산
>>> a = sigmoid(h)시그모이드 함수에 의현 비선형 변환이 가능해짐
출력 a를 활성화(activation)라 하며 또 다른 연결계층으로 연결시킴
improt numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.random.randn(10,2) # 입력
W1 = np.random.randn(2,4) # 가중치
b1 = np.random.randn(4) # 편향
W2 = np.random.randn(4,3) # 가중치
b2 = np.random.randn(3) # 편향
h = np.mutmul(x,W1) + b1
a = sigmoid(h)
s = np.mutmul(a,W2) + b2x의 형상은 (10,2)으로 2차원 데이터 10개가 미니배치로 처리
s의 최종 출력 형상은 (10,3)로 3차원 데이터로 변환
출력된 3차원 벡터의 각 차원은 각 클래스에 대한 점수가 되며, 출력층에서 가장 큰 값을 내뱉는 뉴런에 해당하는 클래스가 예측 결과가 됨
1.2.2 계층으로 클래스화 및 순전파 구현
Affine 계층 - 완전연결계층
Sigmoid 계층 - 시그모이드 함수에 의한 변환
forward() - 기본변환 수행 매서드
순전파(forward propagation) - 신경망 추론 과정에서 하는 처리, 입력층에서 출력층으로 향하는 전파
역전파(backward propagation) - 데이터 기울기를 순전파와 반대방향으로 전파
# coding: utf-8
import numpy as np
class Sigmoid:
def __init__(self):
self.params = []
def forward(self, x):
return 1 / (1 + np.exp(-x))
class Affine:
def __init__(self, W, b):
self.params = [W, b]
def forward(self, x):
W, b = self.params
out = np.dot(x, W) + b
return out
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 가중치와 편향 초기화
W1 = np.random.randn(I, H)
b1 = np.random.randn(H)
W2 = np.random.randn(H, O)
b2 = np.random.randn(O)
# 계층 생성
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
# 모든 가중치를 리스트에 모은다.
self.params = []
for layer in self.layers:
self.params += layer.params
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)
print(s)실행순서
x생성 (10,2) -> TwoLayerNet(2, 4, 3) init 부분 실행 -> s model.predict(x) -> (10,3)에 해당되는 점수가 출력
1.3 신경망의 학습
1.3.1 손실 함수
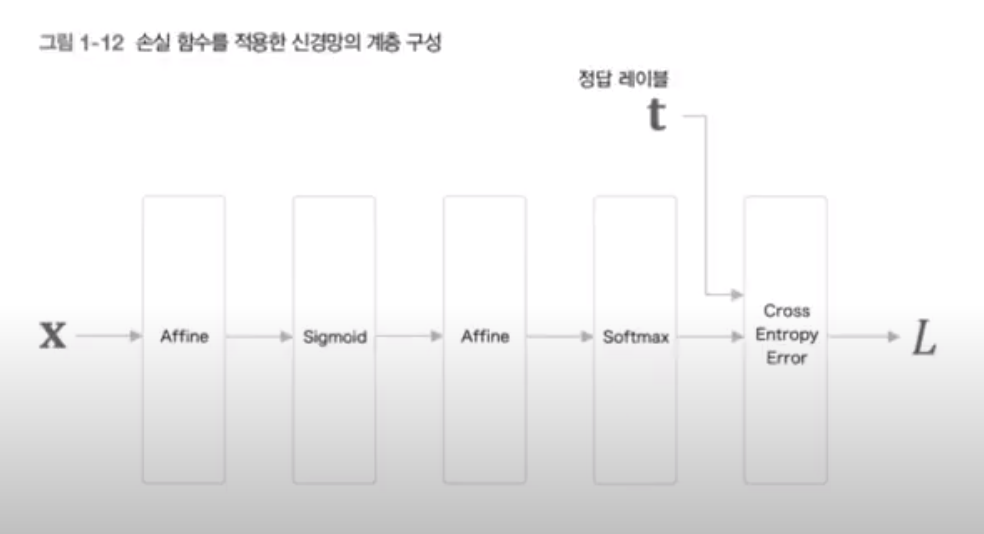
학습의 평가를 위해 손실(loss)을 비교
신경망의 손실은 손실함수를 사용해 구함
다중 클래스 분류(multi-class classification)는 흔히 교차 엔트로피 오차(Cross Entropy error)를 이용
교차엔트로피오차는 '확률'과 '정답레이블'을 이용해 구함
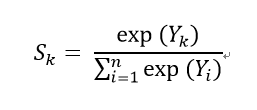
소프트맥스(softmax) 함수
출력이 총 n개 일때 k번째 출력 sk를 구하는 식
점수 sk의 지수함수 / 모든 입력신호의 지수함수의 총합
출력이 0.0 이상 1.0 이하의 실수로 값이 나오고, 총 합은 1임
<sk / 총 합>이기에 확률로 해석 할 수 있음
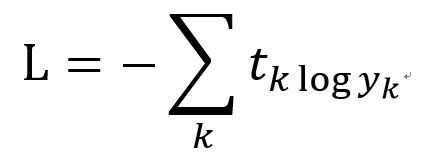
교차 엔트로피 오차 수식
tk는 k번째 클래스에 해당하는 정답 레이블, log는 네이피어 상수 e를 밑으로 하는 로그
정답레이블인 t = [0,0,1]과 같이 0과 1이루어진 원핫 벡터로 표기
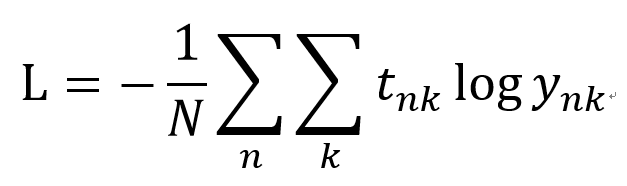
미니배치처리를 고려한 교차엔트로피 오차 수식
위의 수식에서 데이터 N개로 확장
tnk는 n번째 입력데이터에 대한 k번째 클래스 정답 원핫벡터
1/N으로 나누어 평균 손실함수를 구함
1.3.2 미분과 기울기
신경망학습은 손실을 최소화하는 매개변수를 찾는 것
y = f(x) 함수에 대해 x에 대한 y의 미분은 dy/dx
x의 값에 변화에 대한 y의 '변화의 정도' == y에 대한 x의 영향도
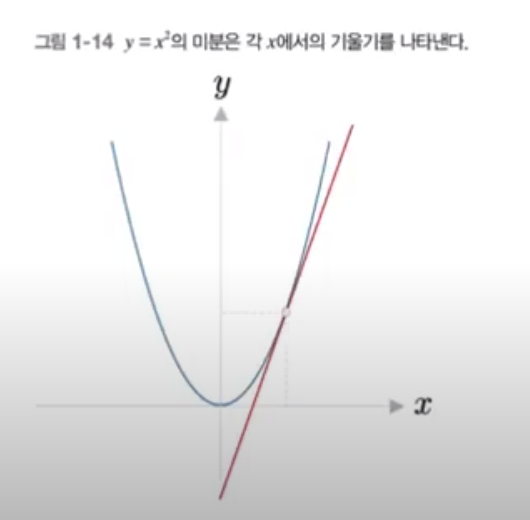
y = x² 함수에서 dy/dx = 2x
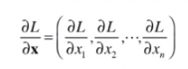
위에서는 1개의 변수에 대한 미분을 구했지만 여러개의 변수도 미분할 수 있음
벡터의 각 원소에 대한 미분을 정리한 것이 기울기
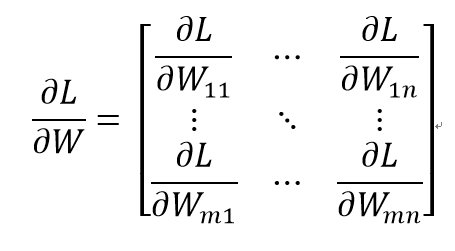
행렬의 기울기
여기서 W와 ∂L/∂W의 형상이 같음 # ∂편미분, 라운드디
'행렬과 기울기의 형상이 같다'는 성질을 이용하면 매개변수 갱신과, 연산법칙을 쉽게 구현 할 수 있음
1.3.3 연쇄 법칙
기울기를 구하기 위해 오차역전파법(vack-propagation) 을 사용
오차역전파법의 핵심은 연쇄법칙(chain rule)
y = f(x) 와 z = g(y) 라는 두 함수가 있다고 가정하면, z = g( f(x) )가 됨
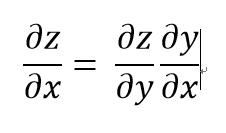
즉 y에 대한 z 미분값과 x에 대한 y 미분값을 곱하면 x에 대한 z 미분값
x가 z에 미치는 영향도를 계산하기 위해서는 y에 대한 z 미분값과 x에 대한 y 미분값을 곱하면 된다.
1.3.4 계산 그래프
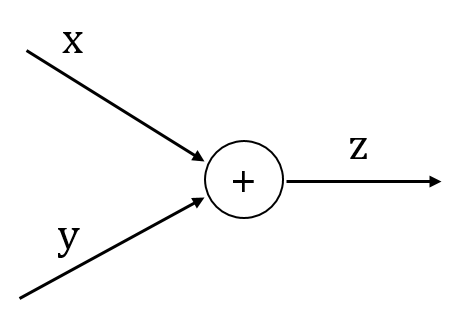
z = x + y를 나타내는 계산 그래프
-> 순전파 <- 역전파
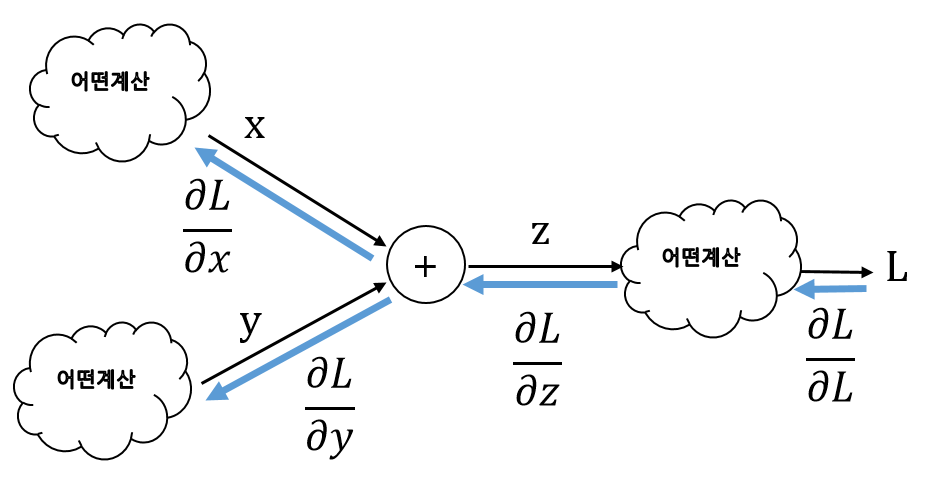
덧셈노드
∂L/∂x 은 x가 L에 미치는 영향
앞에서 배운 연쇄 법칙에 의해 역전파로 흐르는 미분은 상류로 흘러온 미분과 국소적 미분을 곱해 계산
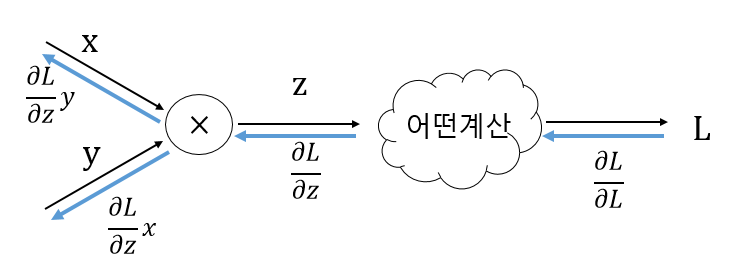
곱셈노드
∂L/∂x = ∂L/∂z ∂z/∂x
∂z/∂x = y
∂L/∂x = ∂L/∂z y
위 노드 계산들은 하나의 데이터 예시지만 벡터,행렬, 텐서 같은 다 변수도 가능하며 독립적으로 원소별 연산을 수행
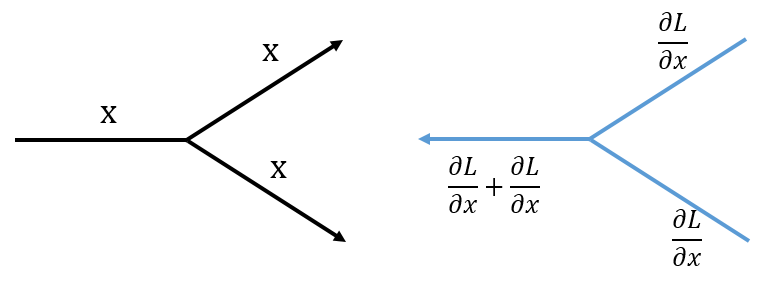
분기노드
단순히 선이 나뉘기에 복제노드라고도 함
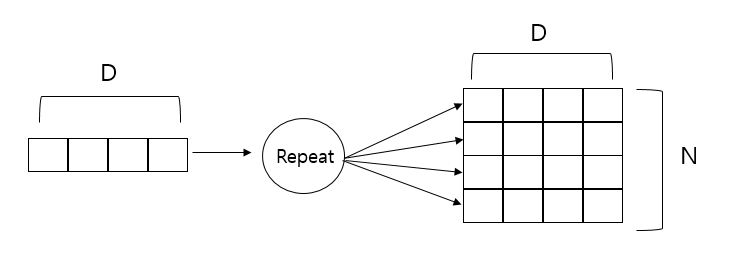
Repeat 노드
위 2개로 나뉘는 분기노드를 N개의 분기로 확장한 것
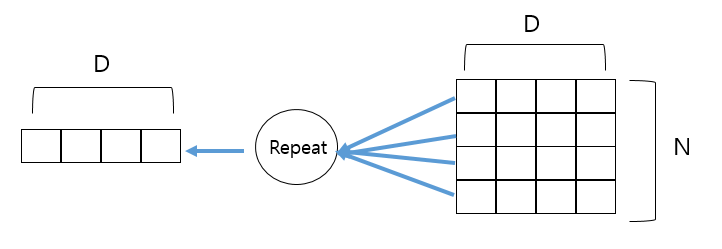
Repeat 노드의 역전파
상역전파는 N개의 미분값(기울기)를 모두 더해 구한다.
>>> import numpy as np
>>> D, N = 8,7
>>> x = np.random.randn(1, D) # 입력
>>> y = repeat(x, N, axis=0) # 순전파 문자열을 반복한 값을 반환
>>> dy = np.random.randn(N, D) # 무작위 기울기
>>> dx = np.sum(dy, axis=0, keepdims=True)) # 역전파
# keepdims=True로 설정하면 축소된 축이 결과에 크기가 1인 차원으로 남고, 결과가 입력 배열에 대해 올바르게 브로드캐스트됨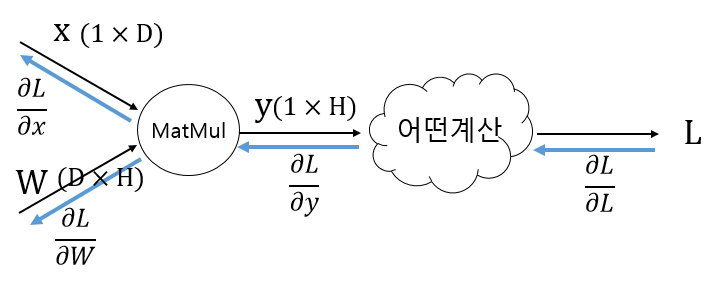
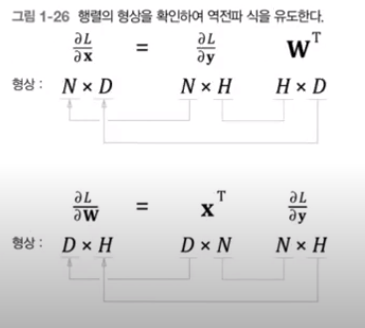
MatMul 노드(matrix multiply의 약자)_p52참조
y = xW에서 x, W, y의 형상은 x : 1 × D, W : D × H, y : 1 × H
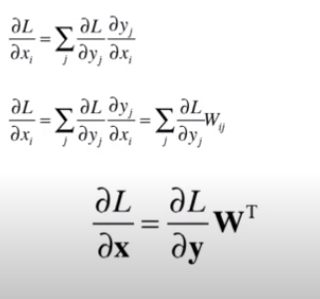
- 역전파 설명
첫번째 식 - x행렬의 i번째 원소에 대한 미분 ∂L/∂xi
xi를 (조금)변화시켰을 때 L이 얼마나 변할 것인가라는 '변화의 정도'
xi가 변하면 y벡터의 모든 원소가 변하고 최종적으로 L도 변함
xi에서 L에 이르는 연쇄법칙의 경로는 여러개이며 그 총합은 ∂L/∂xi임
두번째 식 - ∂yi/∂xi = Wij가 성립하여 대입
세번째 식 - ∂L/∂xi는 벡터∂L/∂y와 W의 i행 벡터의 내적으로 구해지는 점을 이용해 정리
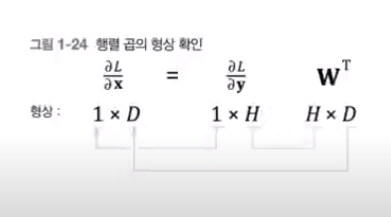
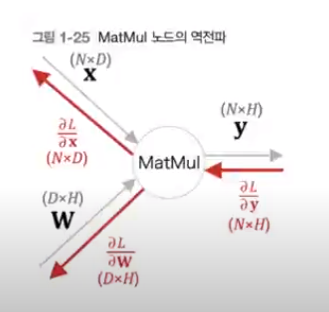
행렬의 역전파도 '순전파 시 입력을 서로 바꾼 값을 이용'
class MatMul:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)] # 떤 변수만큼의 사이즈인 0 으로 가득 찬 Array 생성
self.x = None
def forward(self, x):
W, = self.params
out = np.matmul(x, W)
self.x = x
return out
def backward(self, dout):
W, = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
self.grads[0][...] = dW # [...] 생략기호, 깊은 복사 역활(p55 참조)
return dx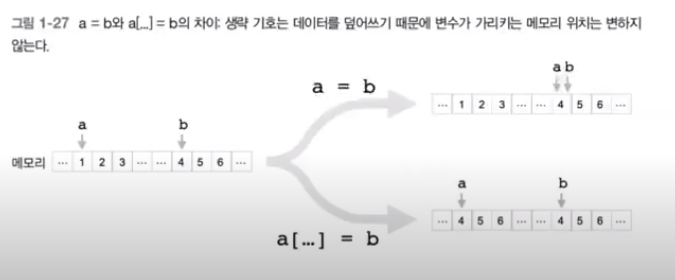
[...]에 대한 차이
위 얕은 복사, 아래 깊은 복사로 메모리 위치 변화에 따른 차이가 있음
1.3.5 기울기 도출과 역전파 구현
각 계층 구현
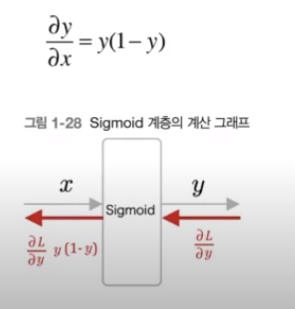
- Sigmoid 계층
식 시그모이드 함수의 미분 ∂L/∂y -> y(1-y) (1권 p169 참조)
class Sigmoid:
def __init__(self):
self.params, self.grads = [], []
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx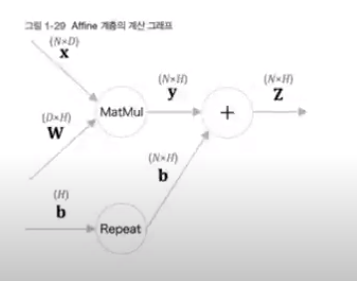
- Affine 계층
순전파 y = np.matmul(x, W) + b(편향을 더할땐 브로드캐스트 적용)
class Affine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
W, b = self.params
out = np.matmul(x, W) + b
self.x = x
return out
def backward(self, dout):
W, b = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dxmatmul과 Repeat노드의 역전파 수행
% 이미 구현한 MatMul 계층을 이용하면 더 쉽게 구현할 수 있음
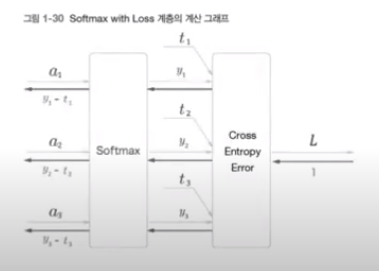
- Softmax with loss계층
Softmax와 교차 엔트로피 오차로 loss를 출력
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실
self.y = None # softmax의 출력
self.t = None # 정답레이블(원-핫 벡터)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y,self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx(코드는 1권 p179,p291 참조)
1.3.6 가중치 갱신
- 신경망 학습 순서
- 미니배치
훈련 데이터 중 무작위로 다수의 데이터를 골라냄 - 기울기 계산
오차역전파법으로 각 가중치 매개변수에 대한 손실함수 기울기를 구함 - 매개변수 갱신
기울기를 사용하여 가중치 매개변수를 갱신 - 반복
1~3단계를 필요한 만큼 반복
- 경사하강법(Gradient Decent)
매개변수의 손실을 가장 크게하는 방향(오차역전파법의 가중치 기울기)과 반대방향으로 갱신하여 손실을 줄이는 방법 - 확률적경사하강법(Stochastic Gradient Decent): 무작위로 서낵된 데이터(미니배치)에 대한 기울기를 이용

가중치에서 학습률과 손실함수의 기울기를 곱한 값을 뺀 값으로 갱신
η(학습률)이며 0.01이나 0.001값으로 미리 정해 사용
class SGD:
def __init__(self,lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]1.4 신경망으로 문제를 풀다
1.4.1 스파이럴 데이터셋
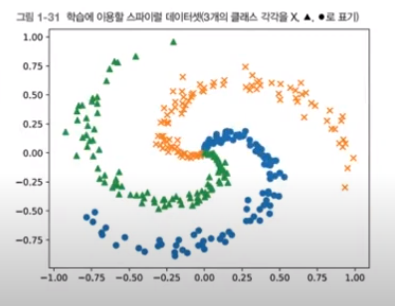
# coding: utf-8
import sys
sys.path.append('..') # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from dataset import spiral
import matplotlib.pyplot as plt
x, t = spiral.load_data()
print('x', x.shape) # (300, 2)
print('t', t.shape) # (300, 3) 3차원 정답 원-핫 벡터
# 데이터점 플롯
N = 100
CLS_NUM = 3
markers = ['o', 'x', '^']
for i in range(CLS_NUM):
plt.scatter(x[i*N:(i+1)*N, 0], x[i*N:(i+1)*N, 1], s=40, marker=markers[i])
plt.show()직선으로 분류할 수 없기 때문에 비선형으로 구해야함
1.4.2 신경망 구현
# coding: utf-8
import sys
sys.path.append('..') # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.layers import Affine, Sigmoid, SoftmaxWithLoss
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 가중치와 편향 초기화
W1 = 0.01 * np.random.randn(I, H)
b1 = np.zeros(H)
W2 = 0.01 * np.random.randn(H, O)
b2 = np.zeros(O)
# 계층 생성
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
self.loss_layer = SoftmaxWithLoss() # 별도 저장
# 모든 가중치와 기울기를 리스트에 모은다.
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def forward(self, x, t):
score = self.predict(x)
loss = self.loss_layer.forward(score, t)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout은닉층이 하나인 신경망
1.4.3 학습용 코드
# coding: utf-8
import sys
sys.path.append('..') # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.optimizer import SGD
from dataset import spiral
import matplotlib.pyplot as plt
from two_layer_net import TwoLayerNet
# 하이퍼파라미터 설정
max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0
# 데이터 읽기, 모델과 옵티마이저 생성
x, t = spiral.load_data()
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)
# 학습에 사용하는 변수
data_size = len(x)
max_iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = []
for epoch in range(max_epoch):
# 데이터 뒤섞기
idx = np.random.permutation(data_size)
x = x[idx]
t = t[idx]
for iters in range(max_iters):
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
# 기울기를 구해 매개변수 갱신
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
# 정기적으로 학습 경과 출력
if (iters+1) % 10 == 0:
avg_loss = total_loss / loss_count
print('| 에폭 %d | 반복 %d / %d | 손실 %.2f'
% (epoch + 1, iters + 1, max_iters, avg_loss))
loss_list.append(avg_loss)
total_loss, loss_count = 0, 0
# 학습 결과 플롯
plt.plot(np.arange(len(loss_list)), loss_list, label='train')
plt.xlabel('반복 (x10)')
plt.ylabel('손실')
plt.show()
# 경계 영역 플롯
h = 0.001
x_min, x_max = x[:, 0].min() - .1, x[:, 0].max() + .1
y_min, y_max = x[:, 1].min() - .1, x[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
X = np.c_[xx.ravel(), yy.ravel()]
score = model.predict(X)
predict_cls = np.argmax(score, axis=1)
Z = predict_cls.reshape(xx.shape)
plt.contourf(xx, yy, Z)
plt.axis('off')
# 데이터점 플롯
x, t = spiral.load_data()
N = 100
CLS_NUM = 3
markers = ['o', 'x', '^']
for i in range(CLS_NUM):
plt.scatter(x[i*N:(i+1)*N, 0], x[i*N:(i+1)*N, 1], s=40, marker=markers[i])
plt.show()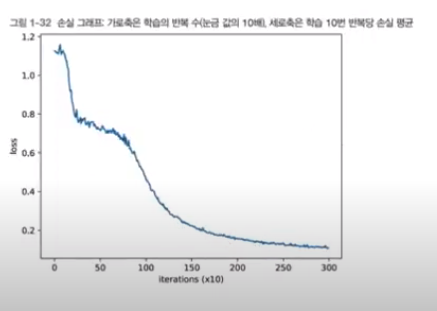
실행시킨 결과

시각화_결정경계(decision boundary)
1.4.4 Trainer 클래스
# coding: utf-8
import sys
sys.path.append('..') # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from common.optimizer import SGD
from common.trainer import Trainer
from dataset import spiral
from two_layer_net import TwoLayerNet
# 하이퍼파라미터 설정
max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0
x, t = spiral.load_data()
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)
trainer = Trainer(model, optimizer)
trainer.fit(x, t, max_epoch, batch_size, eval_interval=10)
trainer.plot()1.5 계산 고속화
1.5.1 비트 정밀도
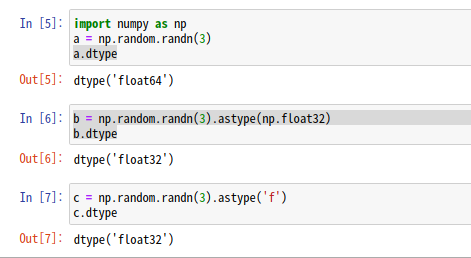
기본적으로 64비트 부동소수점 수가 사용됨
신경망 추론과 학습은 32비트에서도 수행되며 용량도 절반 사용됨
1.5.2 GPU(쿠파이)
import cupy as cp
x = cp.arange(6).reshape(2,3).astype('f')GPU를 사용하여 병렬 계산을 빠르게 처리 가능
1.5 정리
- 신경망은 입력층, 은닉층(중간층), 출력층을 지닌다.
- 완전연결계층에 의한 선형 변환이 이뤄지고, 활성화 함수에 의해 비선형 변환이 이뤄진다.
- 완전연결계층이나 미니배치 처리는 행렬로 모아 한꺼번에 계산할 수 있다.
- 오차역전파법을 사용하여 신경망 손실에 관한 기울기를 효율적으로 구할 수 있다.
- 신경망이 수행하는 처리는 계산 그래프로 시각화할 수 있으며, 순전파와 역전파를 이해하는 데 도움이 된다.
- 신경망의 구성요소들을 '계층'으로 모듈화해두면, 이를 조립하여 신경망을 쉽게 구성할 수 있다.
- 신경망 고속화에는 GPU를 이용한 병렬 계산과 데이터의 비트 정밀도가 중요하다.
'독서 > 밑바닥부터 시작하는 딥러닝 2' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝 2]Chapter 6. 게이트가 추가된 RNN (0) | 2024.07.30 |
|---|---|
| [밑바닥부터 시작하는 딥러닝 2] Chapter 5. 순환 신경망(RNN) (6) | 2024.07.23 |
| [밑바닥부터 시작하는 딥러닝 2] Chapter 4. word2vec 속도개선 (0) | 2024.07.14 |
| [밑바닥부터 시작하는 딥러닝 2] Chapter 3. word2vec (0) | 2024.07.07 |
| [밑바닥부터 시작하는 딥러닝 2] Chapter 2. 자연어와 단어의 분산 표현 (1) | 2024.06.30 |